通訊系統參考資料:New Bing
參考資料:ChatGPT
請利用ChatGPT來幫助你回答以下的問題,我們將運用通訊問題來達成編解碼。以下是10個問題組合,涵蓋不同的編解碼技術和概念:

給定一個Hamming(7,4)編碼,請找出所有可能的錯誤並糾正它們。

Hamming(7,4)編碼是一種用於在數據通信和錯誤校驗中進行數據編碼的技術。它由Richard Hamming在1950年代早期發明,可將4位數據位轉換為7位編碼。該編碼方案基於奇偶校驗位的概念,並且可以用於檢測和糾正單位錯誤。
具體而言,Hamming(7,4)編碼方案將4位數據位(D1,D2,D3,D4)轉換為7位編碼(D1,D2,D3,P1,D4,P2,P3),其中P1,P2和P3是奇偶校驗位,它們的值由數據位和其他奇偶校驗位的值決定。
具體來說,P1的值是D1,D2,D3的奇偶性,P2的值是D1,D2,D4的奇偶性,P3的值是D2,D3,D4的奇偶性。這種編碼方案可以檢測和糾正單位錯誤,並且可以通過添加額外的奇偶校驗位來檢測更多的錯誤。
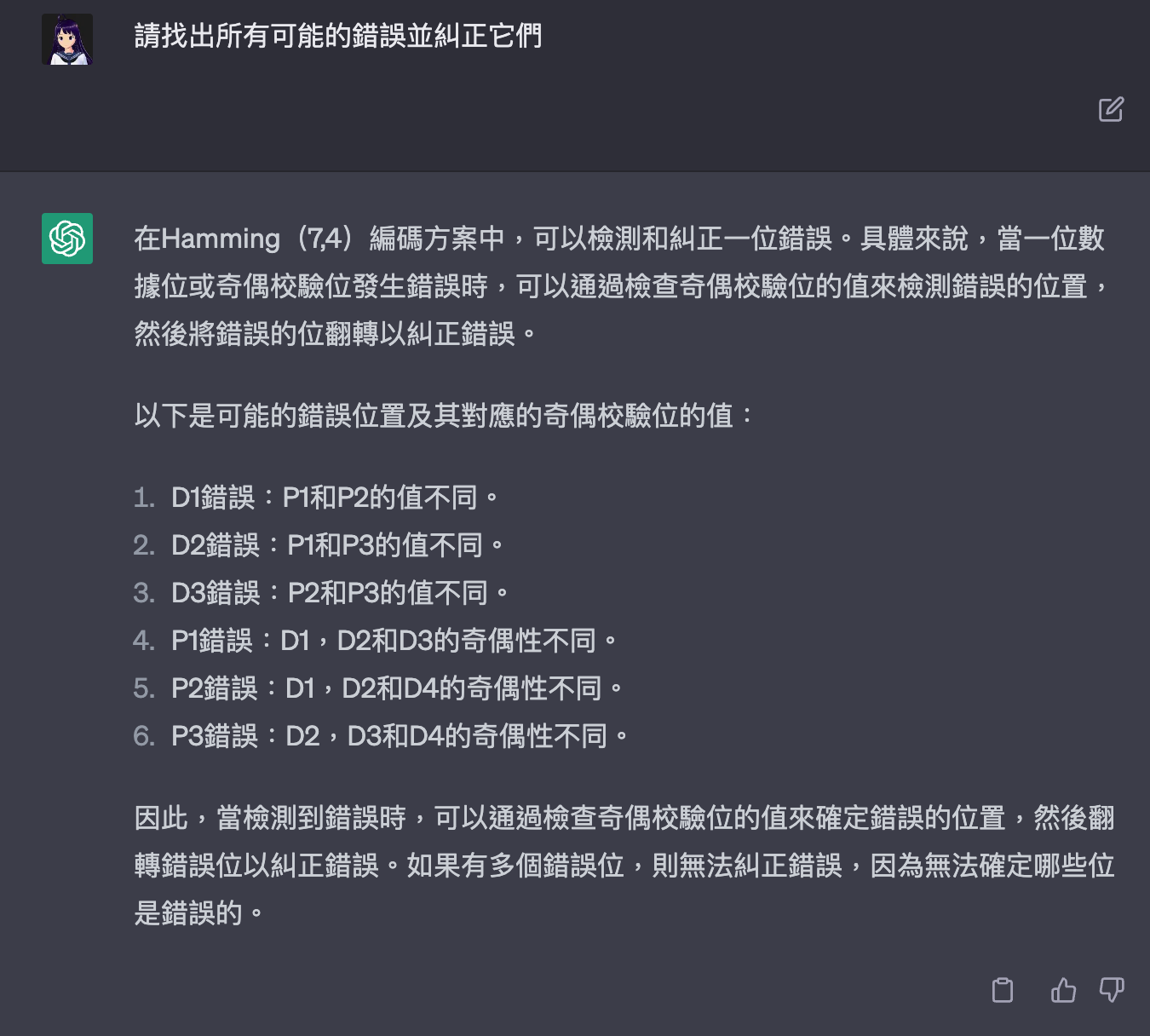
在Hamming(7,4)編碼方案中,可以檢測和糾正一位錯誤。具體來說,當一位數據位或奇偶校驗位發生錯誤時,可以通過檢查奇偶校驗位的值來檢測錯誤的位置,然後將錯誤的位翻轉以糾正錯誤。
以下是可能的錯誤位置及其對應的奇偶校驗位的值:
因此,當檢測到錯誤時,可以通過檢查奇偶校驗位的值來確定錯誤的位置,然後翻轉錯誤位以糾正錯誤。如果有多個錯誤位,則無法糾正錯誤,因為無法確定哪些位是錯誤的。
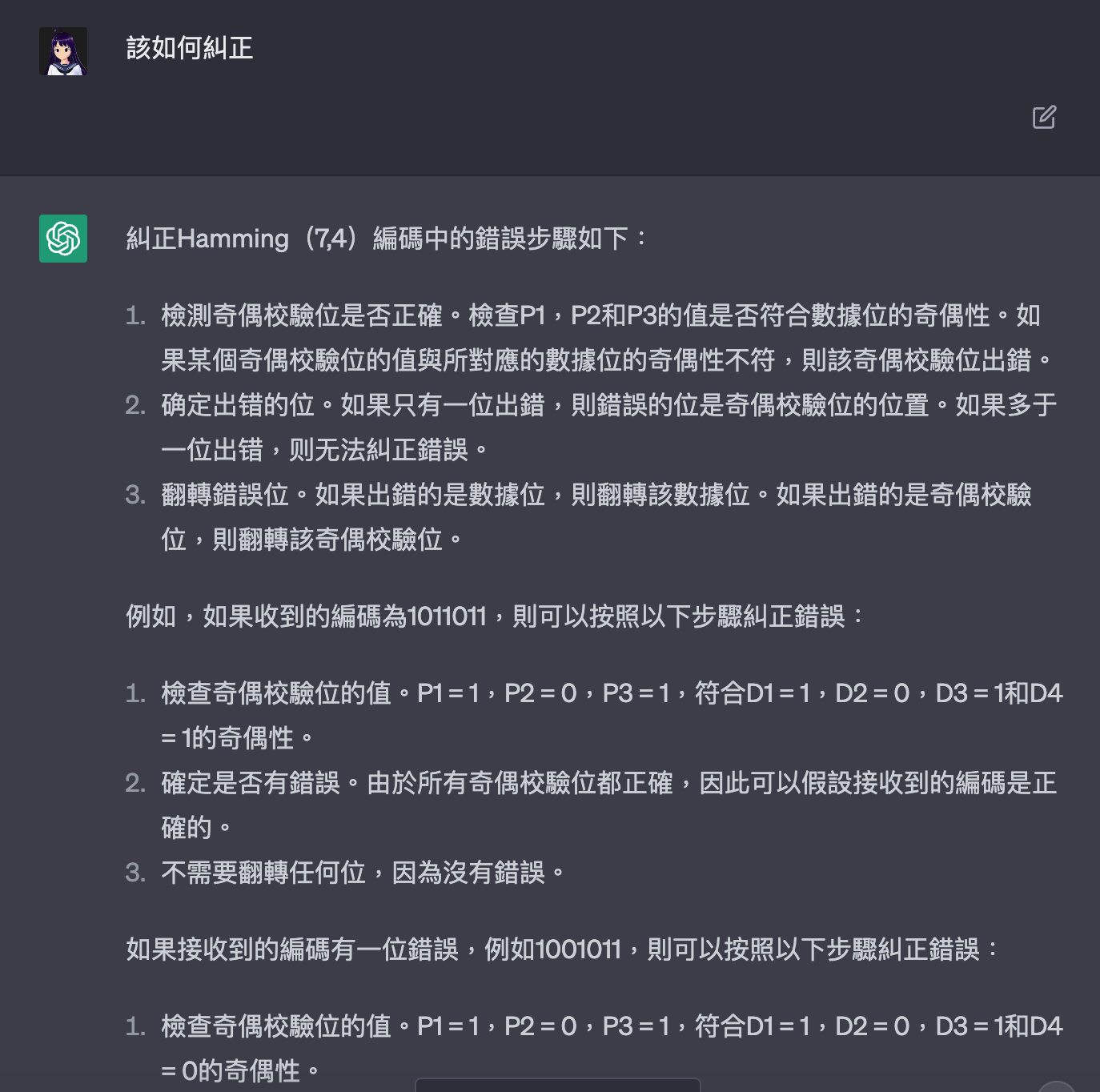
糾正Hamming(7,4)編碼中的錯誤步驟如下:
檢測奇偶校驗位是否正確。檢查P1,P2和P3的值是否符合數據位的奇偶性。如果某個奇偶校驗位的值與所對應的數據位的奇偶性不符,則該奇偶校驗位出錯。
确定出错的位。如果只有一位出錯,則錯誤的位是奇偶校驗位的位置。如果多於一位出错,则無法糾正錯誤。
翻轉錯誤位。如果出錯的是數據位,則翻轉該數據位。如果出錯的是奇偶校驗位,則翻轉該奇偶校驗位。
例如,如果收到的編碼為1011011,則可以按照以下步驟糾正錯誤:
檢查奇偶校驗位的值。P1 = 1,P2 = 0,P3 = 1,符合D1 = 1,D2 = 0,D3 = 1和D4 = 1的奇偶性。
確定是否有錯誤。由於所有奇偶校驗位都正確,因此可以假設接收到的編碼是正確的。
不需要翻轉任何位,因為沒有錯誤。
如果接收到的編碼有一位錯誤,例如1001011,則可以按照以下步驟糾正錯誤:
檢查奇偶校驗位的值。P1 = 1,P2 = 0,P3 = 1,符合D1 = 1,D2 = 0,D3 = 1和D4 = 0的奇偶性。
確定錯誤位的位置。由於P2的值應為0,但接收到的值是1,因此可以得出出錯的位置是D4。
翻轉錯誤位。將D4的值從0翻轉為1,得到正確的數據為1011011。



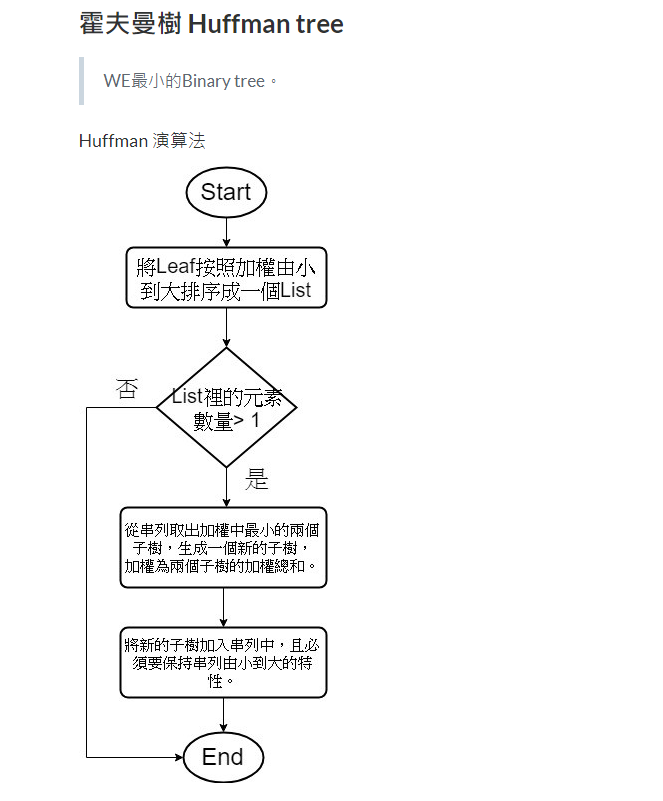
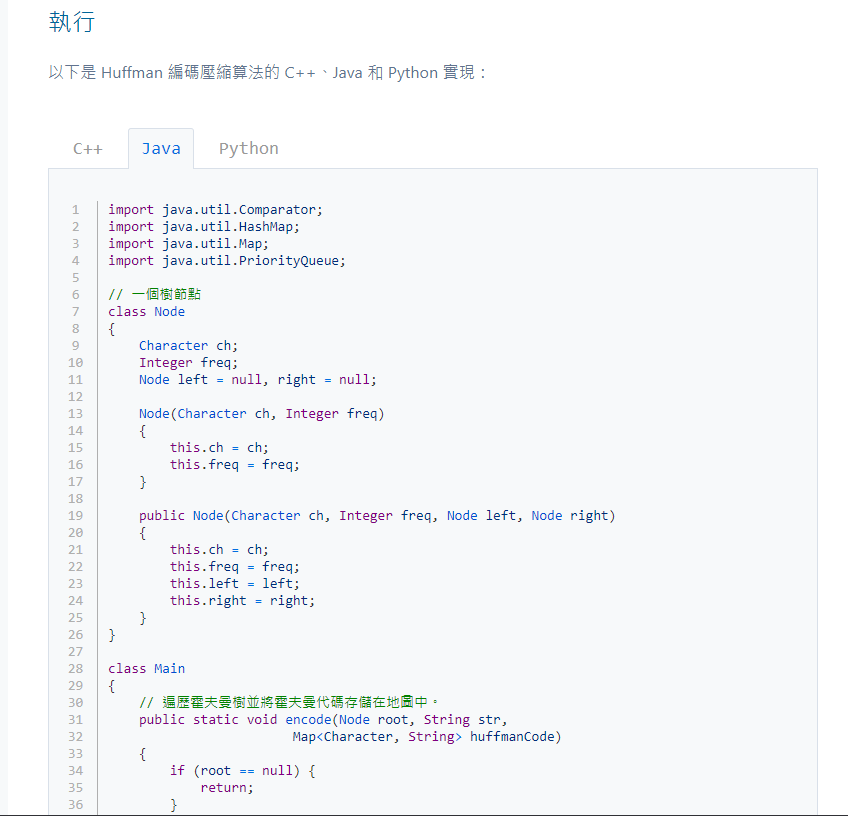
設計一個Huffman編碼樹來壓縮一段英文文章(自行設計),並計算壓縮率。
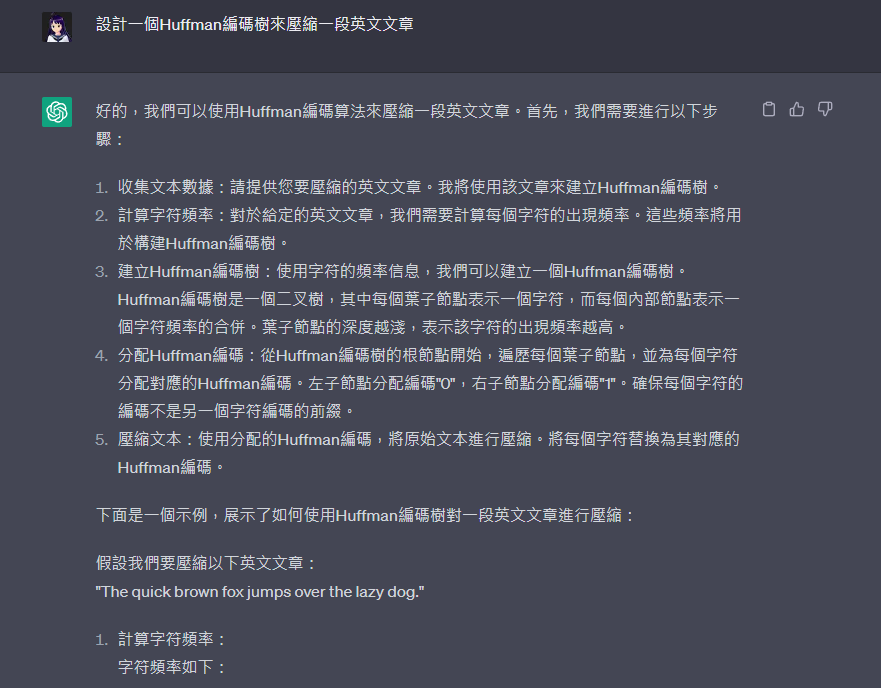
好的,我們可以使用Huffman編碼算法來壓縮一段英文文章。首先,我們需要進行以下步驟:
收集文本數據:請提供您要壓縮的英文文章。我將使用該文章來建立Huffman編碼樹。
計算字符頻率:對於給定的英文文章,我們需要計算每個字符的出現頻率。這些頻率將用於構建Huffman編碼樹。
建立Huffman編碼樹:使用字符的頻率信息,我們可以建立一個Huffman編碼樹。Huffman編碼樹是一個二叉樹,其中每個葉子節點表示一個字符,而每個內部節點表示一個字符頻率的合併。葉子節點的深度越淺,表示該字符的出現頻率越高。
分配Huffman編碼:從Huffman編碼樹的根節點開始,遍歷每個葉子節點,並為每個字符分配對應的Huffman編碼。左子節點分配編碼"0",右子節點分配編碼"1"。確保每個字符的編碼不是另一個字符編碼的前綴。
壓縮文本:使用分配的Huffman編碼,將原始文本進行壓縮。將每個字符替換為其對應的Huffman編碼。
下面是一個示例,展示了如何使用Huffman編碼樹對一段英文文章進行壓縮:
假設我們要壓縮以下英文文章:
"The quick brown fox jumps over the lazy dog."
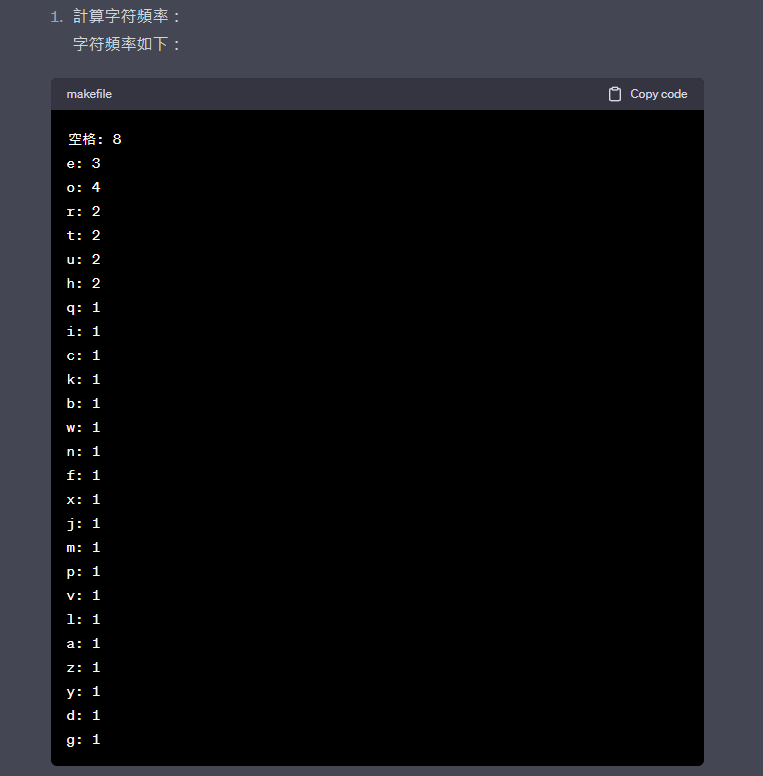
計算字符頻率:
字符頻率如下:空格: 8 e: 3 o: 4 r: 2 t: 2 u: 2 h: 2 q: 1 i: 1 c: 1 k: 1 b: 1 w: 1 n: 1 f: 1 x: 1 j: 1 m: 1 p: 1 v: 1 l: 1 a: 1 z: 1 y: 1 d: 1 g: 1
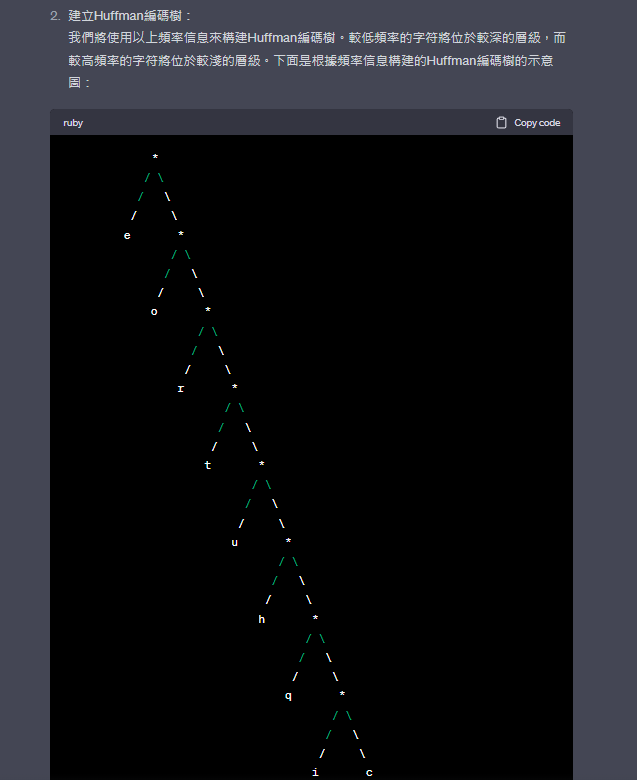
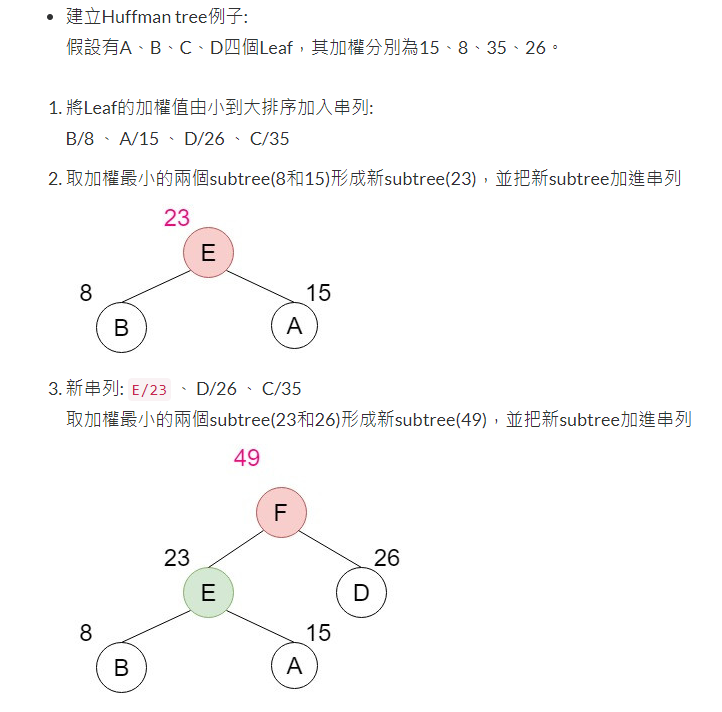
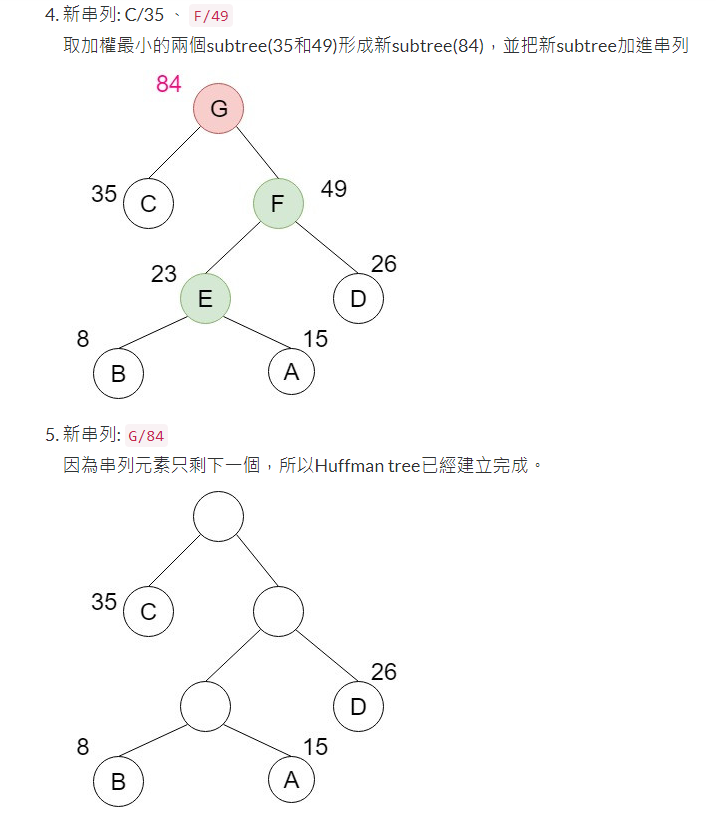
建立Huffman編碼樹:
我們將使用以上頻率信息來構建Huffman編碼樹。較低頻率的字符將位於較深的層級,而較高頻率的字符將位於較淺的層級。下面是根據頻率信息構建的Huffman編碼樹的示意圖:
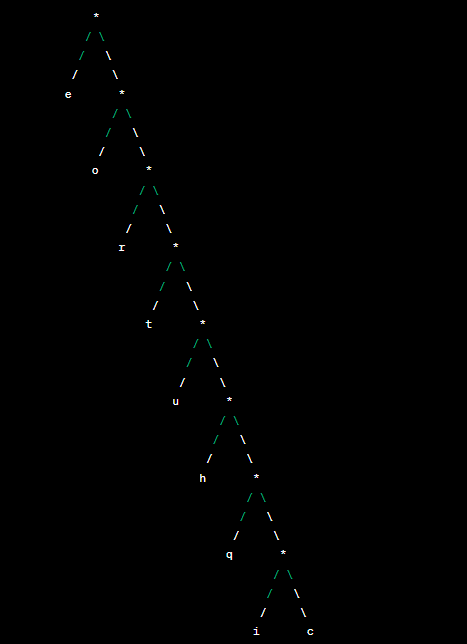
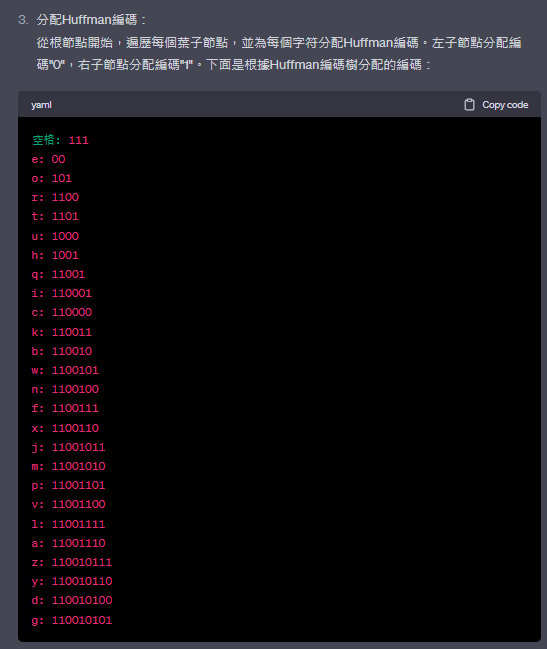
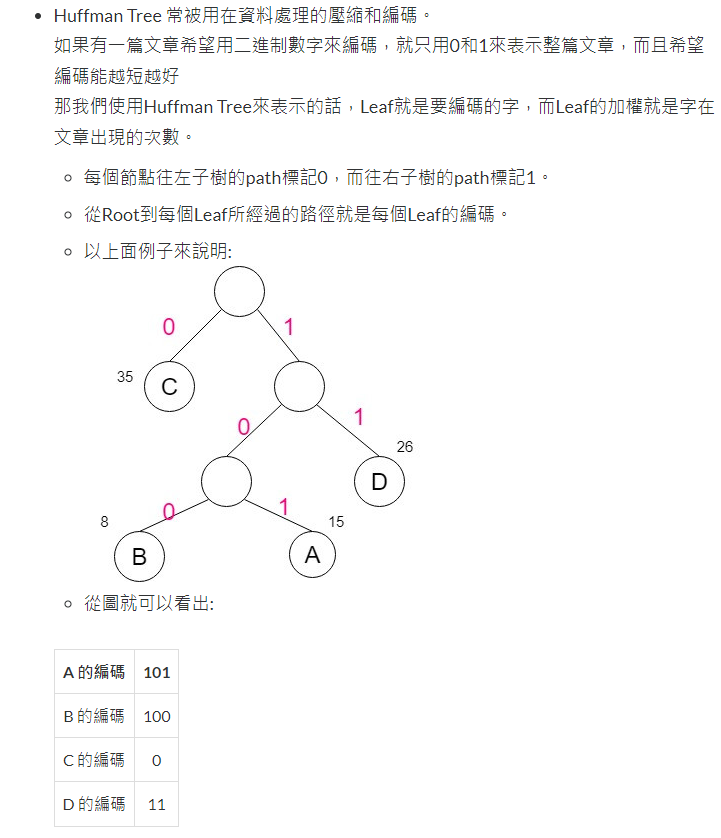
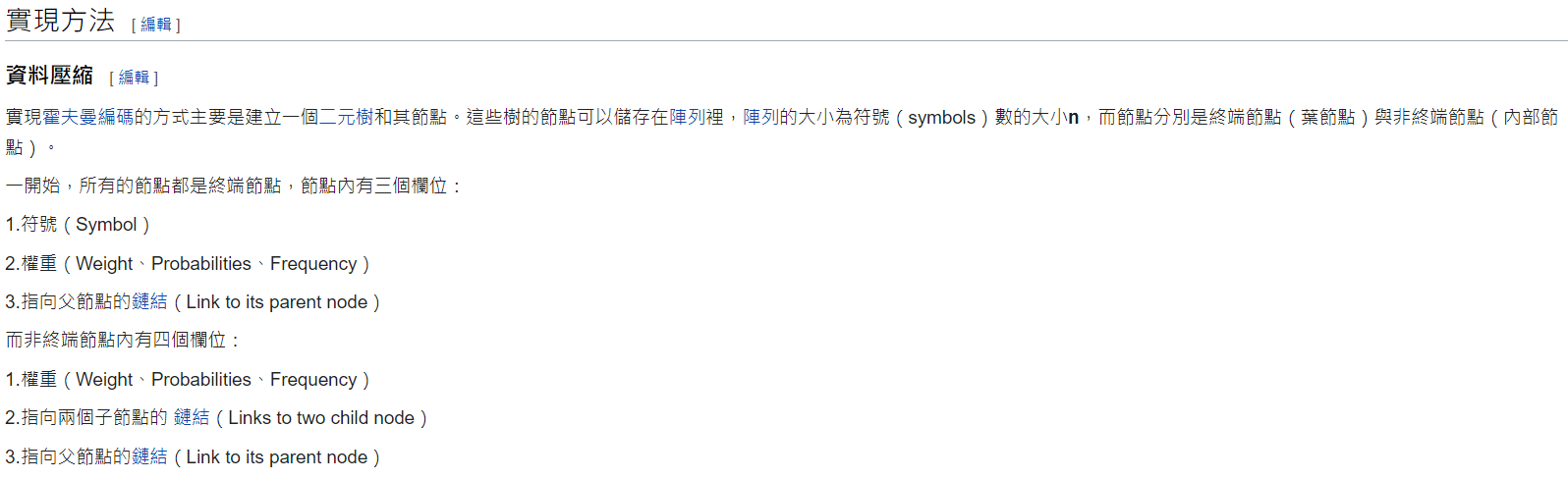
分配Huffman編碼:
從根節點開始,遍歷每個葉子節點,並為每個字符分配Huffman編碼。左子節點分配編碼"0",右子節點分配編碼"1"。下面是根據Huffman編碼樹分配的編碼: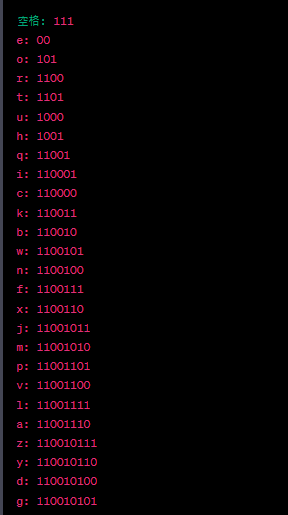
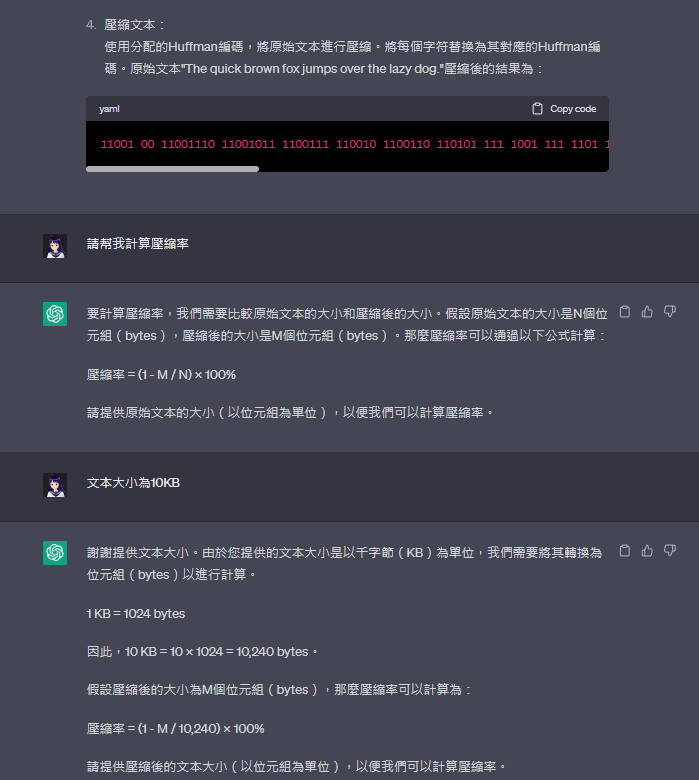
壓縮文本:
使用分配的Huffman編碼,將原始文本進行壓縮。將每個字符替換為其對應的Huffman編碼。原始文本"The quick brown fox jumps over the lazy dog."壓縮後的結果為:
11001 00 11001110 11001011 1100111 110010 1100110 110101 111 1001 111 1101 111 00 110011 101 11001111 110010 1000 111 1100101 110010100 101 1100100 1001 110010 1001 101 1100 111 1100111 11001010 1001 11001011 110010111 101 110011
要計算壓縮率,我們需要比較原始文本的大小和壓縮後的大小。假設原始文本的大小是N個位元組(bytes),壓縮後的大小是M個位元組(bytes)。那麼壓縮率可以通過以下公式計算:
壓縮率 = (1 - M / N) × 100%
請提供原始文本的大小(以位元組為單位),以便我們可以計算壓縮率。
謝謝提供文本大小。由於您提供的文本大小是以千字節(KB)為單位,我們需要將其轉換為位元組(bytes)以進行計算。
1 KB = 1024 bytes
因此,10 KB = 10 × 1024 = 10,240 bytes。
假設壓縮後的大小為M個位元組(bytes),那麼壓縮率可以計算為:
壓縮率 = (1 - M / 10,240) × 100%
請提供壓縮後的文本大小(以位元組為單位),以便我們可以計算壓縮率。
謝謝提供壓縮後文本的大小。同樣地,我們需要將其轉換為位元組(bytes)以進行計算。
1 KB = 1024 bytes
因此,1 KB = 1 × 1024 = 1,024 bytes。
現在,我們有原始文本的大小為10,240 bytes,壓縮後的文本大小為1,024 bytes。
壓縮率 = (1 - 1,024 / 10,240) × 100%
= (1 - 0.1) × 100%
= 0.9 × 100%
= 90%
因此,根據提供的資訊,壓縮率為90%。這表示壓縮後的文本大小僅為原始文本大小的10%。

| 例子(前) | 例子(後) |
|---|---|
 |
 |
 |


解釋如何使用低密度奇偶校驗碼(Low-Density Parity-Check, LDPC)進行編碼和解碼,並提供一個範例。


低密度奇偶校驗碼(Low-Density Parity-Check, LDPC)是一種用於編碼和解碼數據的錯誤檢測和糾正技術。它是一種線性塊碼,通過在數據中引入冗餘位進行校驗,可以檢測和糾正傳輸過程中的錯誤。
確定碼字長度:首先確定要編碼的數據的碼字長度,這將決定編碼後的數據長度。
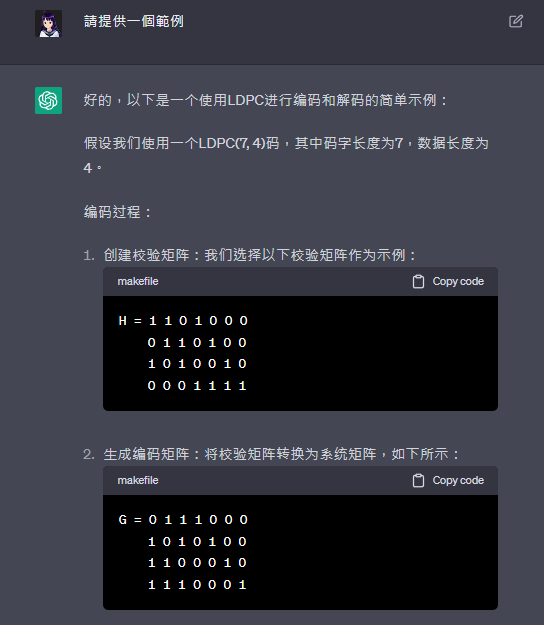
創建校驗矩陣:根據所選擇的LDPC碼的類型和參數,創建一個稀疏的校驗矩陣。校驗矩陣的大小為(n, k),其中n是碼字長度,k是數據長度。
生成編碼矩陣:通過將校驗矩陣轉換為系統矩陣,可以生成編碼矩陣。系統矩陣是一個稀疏矩陣,其中包含了要進行編碼的數據和冗餘位之間的關係。
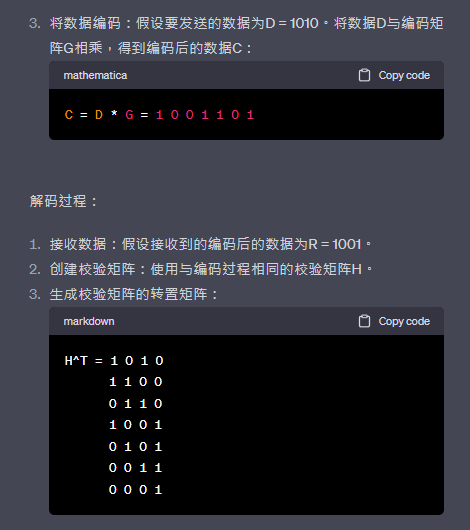
將數據編碼:將要發送的數據乘以編碼矩陣,得到編碼後的數據。編碼後的數據將包括原始數據和冗餘位,以便進行錯誤檢測和糾正。
接收數據:接收通過信道傳輸的編碼後的數據。
創建校驗矩陣:根據所選擇的LDPC碼的類型和參數,創建相應的校驗矩陣。
生成校驗矩陣的轉置矩陣:將校驗矩陣轉置得到轉置矩陣。
迭代解碼:使用迭代解碼算法對接收到的編碼後的數據進行解碼。迭代解碼算法基於信息傳遞的原理,在每個迭代步驟中,將接收到的數據與校驗矩陣的轉置矩陣相乘,並對結果進行處理,以更新數據的估計值。
判斷解碼結果:在每次迭代後,可以通過計算殘餘誤差或檢查校驗位來評估解碼結果的質量。如果殘餘誤差小於預設的閾值,或者所有的校驗位都通過了檢查,則可以認為解碼成功。
輸出解碼結果:如果解碼成功,輸出解碼後的數據;否則,根據需要進行錯誤糾正或報錯。
LDPC碼的性能取決於校驗矩陣的設計和迭代解碼算法的選擇。通過選擇適當的碼長、碼率和迭代次數,可以平衡解碼性能和計算複雜度,從而實現高效的編碼和解碼過程。
好的,以下是一個使用LDPC進行編碼和解碼的簡單示例:
假設我們使用一個LDPC(7, 4)碼,其中碼字長度為7,數據長度為4。
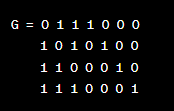
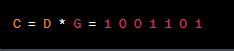
解碼過程:
接收數據:假設接收到的編碼後的數據為R = 1001。
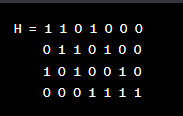
創建校驗矩陣:使用與編碼過程相同的校驗矩陣H。
生成校驗矩陣的轉置矩陣:
迭代解碼:使用迭代解碼算法對接收到的數據R進行解碼。我們可以使用迭代譯碼算法,例如消息傳遞算法(Message Passing Algorithm)。
判斷解碼結果:在每次迭代後,可以計算殘差誤差或檢查校驗位,以評估解碼結果的質量。如果殘差誤差小於預設的閾值,或者所有的校驗位通過了檢查,則可以認為解碼成功。
輸出解碼結果:如果解碼成功,輸出解碼後的數據;否則,根據需要進行錯誤糾正或報錯。
請注意,這只是一個簡單的示例,實際中的LDPC碼通常具有更大的碼字長度和數據長度,並且需要更複雜的迭代解碼算法來實現更好的性能。
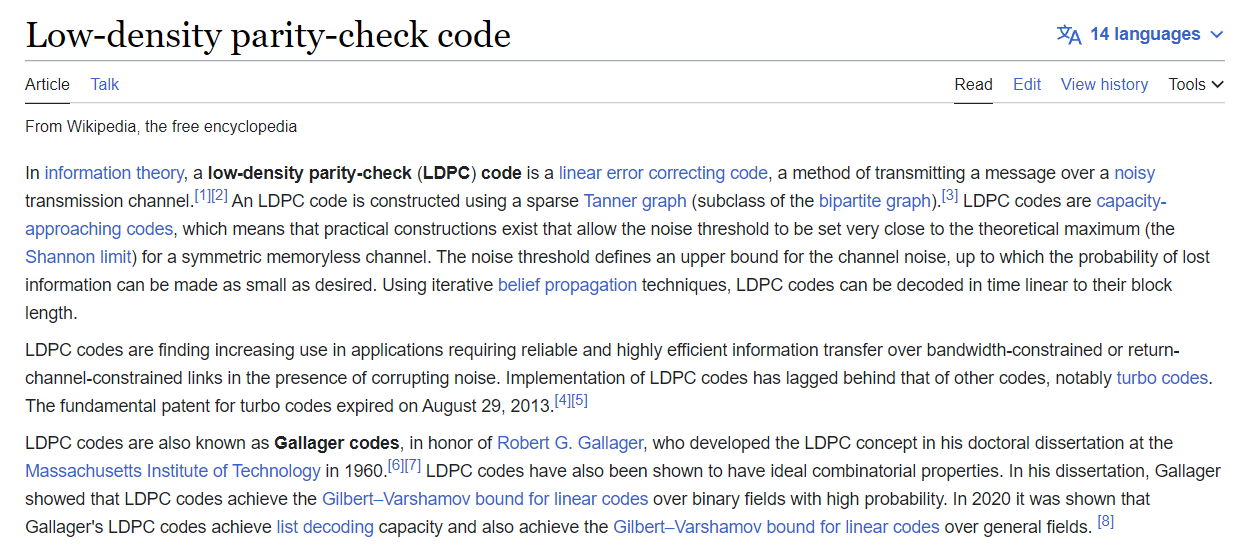

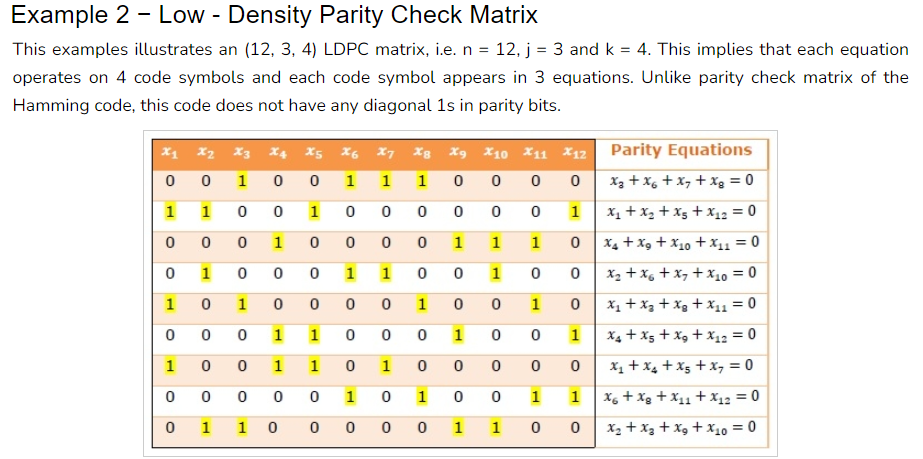

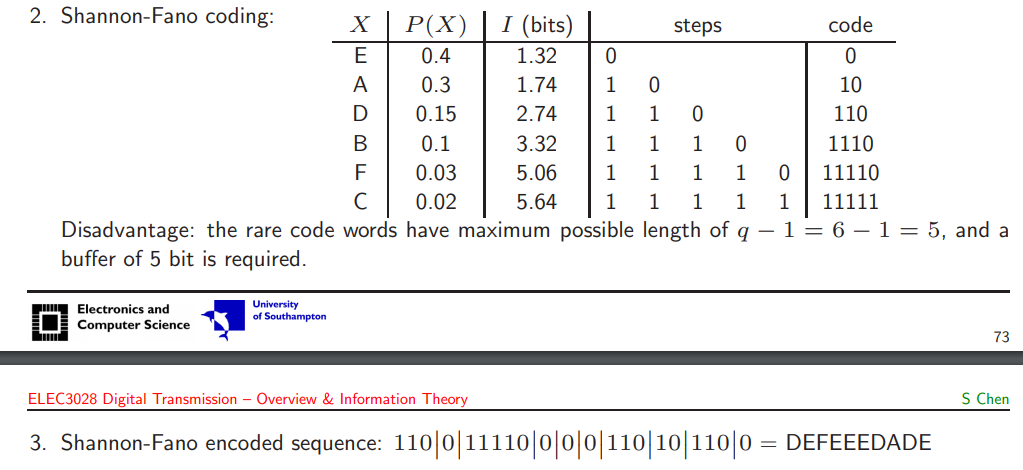
解釋Shannon-Fano編碼的工作原理,並使用它來編碼一段給定的文本(文本請自行設計)。\

Shannon-Fano編碼是一種基於概率的數據壓縮技術,由Claude Shannon和Robert Fano於1948年提出。它的工作原理是根據數據中每個符號出現的概率分配不同長度的編碼,以實現數據的有效壓縮。
以下是Shannon-Fano編碼的工作原理:
計算符號概率:首先,需要計算數據中每個符號的出現概率。這可以通過統計數據中每個符號的頻率並除以總符號數來實現。概率值通常以分數或小數形式表示。
排序符號:根據符號的概率值,將符號按照概率從大到小進行排序。這是為了在後續步驟中,為高頻率的符號分配短的編碼,為低頻率的符號分配長的編碼。
劃分編碼:開始時,將所有的符號分為兩個子集,一個在上半部分,一個在下半部分。上半部分的符號賦予編碼"0",下半部分的符號賦予編碼"1"。
遞歸劃分:對於每個子集,遞歸地重複第3步,直到每個子集中只包含一個符號為止。在每次劃分時,根據符號的概率,將子集一分為二,將上半部分的符號編碼為原編碼後添加"0",將下半部分的符號編碼為原編碼後添加"1"。
生成編碼:通過將每個符號的遞歸劃分路徑上的所有編碼連接起來,生成每個符號的最終編碼。每個符號的編碼將是一個由"0"和"1"組成的字符串,其中"0"表示向上移動,"1"表示向下移動。
解碼數據:對於接收到的編碼數據,開始時從編碼序列的開頭開始,根據編碼的規則進行解碼。將解碼的符號與原始的符號集進行比較,如果找到匹配的符號,則輸出該符號,並從編碼序列中刪除已解碼的部分。然後,繼續從剩餘編碼的開頭開始解碼,直到所有編碼都被解碼為止。
數據壓縮:通過將原始數據用其對應的Shannon-Fano編碼替換,可以實現數據的壓縮。壓縮率取決於符號的概率分佈,即出現頻率高的符號將具有較短的編碼,而出現頻率低的符號將具有較長的編碼。如果數據中的符號按照概率分佈較為均勻,則壓縮效果可能較差。
需要注意的是,Shannon-Fano編碼不一定能實現最優的數據壓縮效果。在一些情況下,會出現編碼後的數據比原始數據更大的情況。這是因為Shannon-Fano編碼並沒有利用符號之間的相關性或統計特性來進一步減小編碼長度。為了實現更高效的壓縮,可以使用其他編碼技術,如Huffman編碼或Arithmetic編碼,它們在一定條件下能夠提供更好的壓縮效果。
總結來說,Shannon-Fano編碼是一種基於概率的數據壓縮技術,通過根據符號的概率分配不同長度的編碼來實現數據的壓縮。它的原理是根據符號的出現概率將符號集遞歸地劃分為兩個子集,並為每個子集賦予不同的編碼。儘管Shannon-Fano編碼相對簡單,但它提供了一種基本的數據壓縮方法,為後續更高級的編碼算法奠定了基礎。
"On behalf of the great state of Illinois, crossroads of a nation, Land of Lincoln, let me express my deepest gratitude for the privilege of addressing this convention. Tonight is a particular honor for me because, let's face it, my presence on this stage is pretty unlikely. My father was a foreign student, born and raised in a small village in Kenya. He grew up herding goats, went to school in a tin-roof shack. His father—my grandfather—was a cook, a domestic servant to the British. But my grandfather had larger dreams for his son. Through hard work and perseverance my father got a scholarship to study in a magical place, America, that shone as a beacon of freedom and opportunity to so many who had come before."
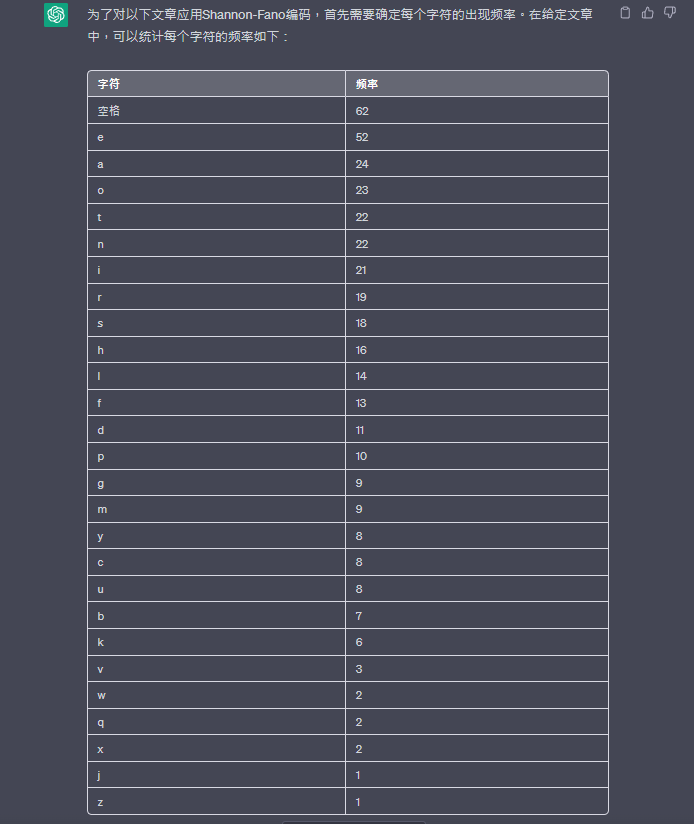
為了對以下文章應用Shannon-Fano編碼,首先需要確定每個字符的出現頻率。在給定文章中,可以統計每個字符的頻率如下:
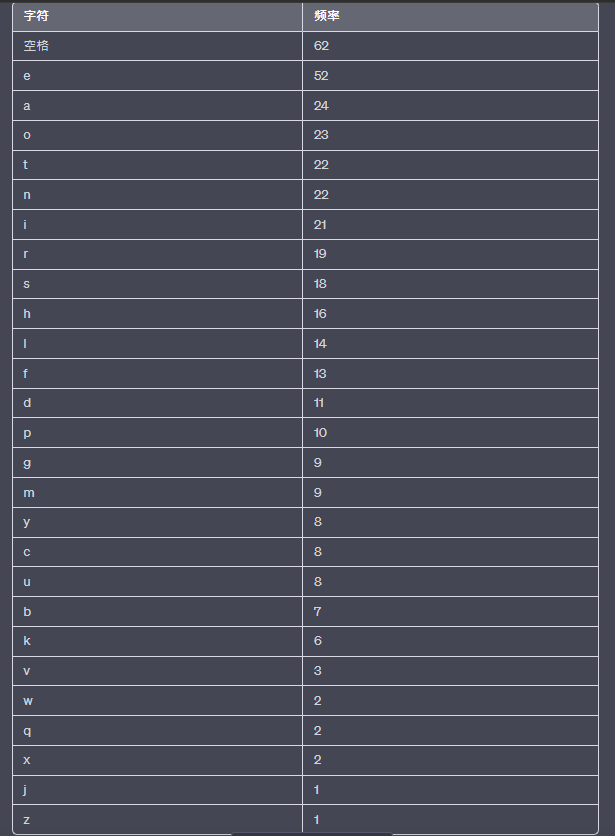
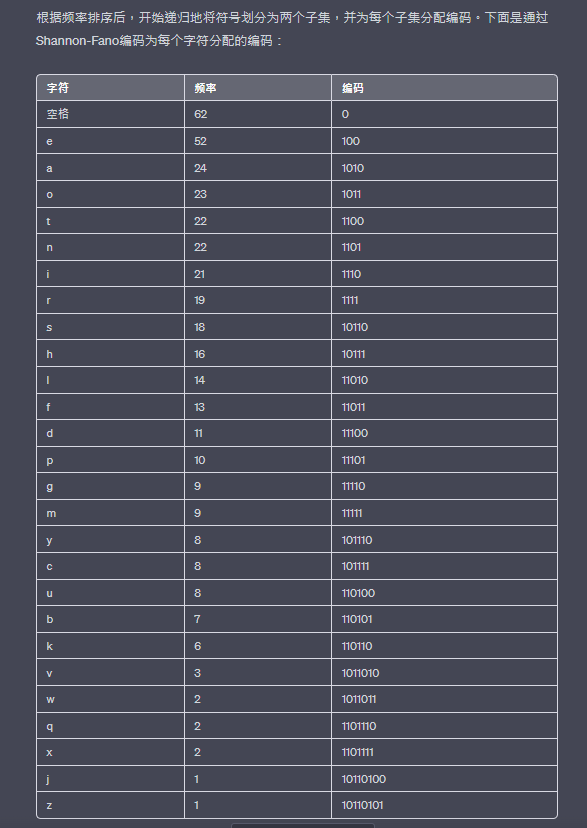
根據頻率排序後,開始遞歸地將符號劃分為兩個子集,並為每個子集分配編碼。下面是通過Shannon-Fano編碼為每個字符分配的編碼:
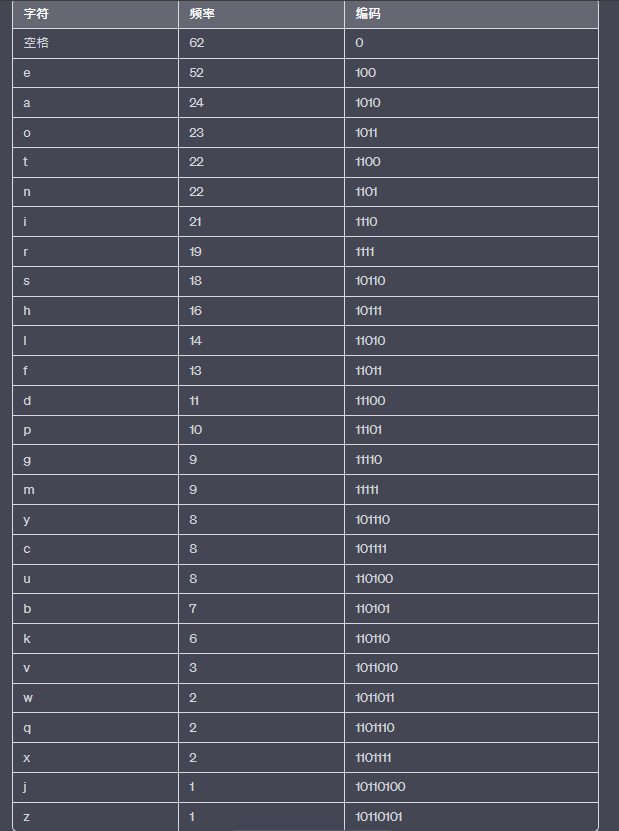
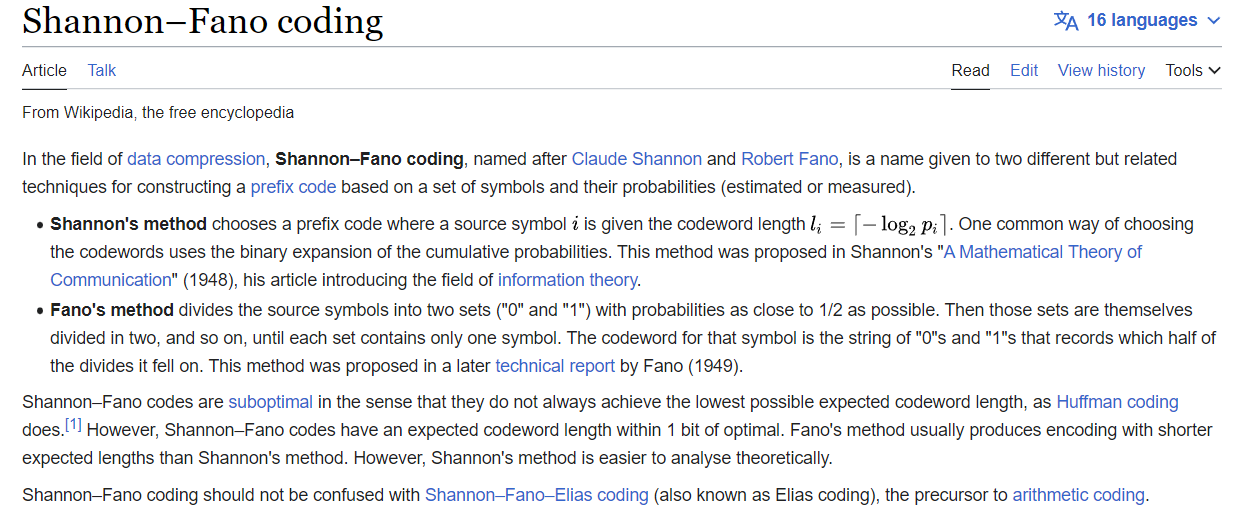
使用上述編碼表,可以將原始文章進行Shannon-Fano編碼。編碼後的結果如下:
"100 11110 101 10110 0 110101 1110 1110 1101111 11100 1010 1111 10110 101 1100 0 110100 1100 101110 11100 1110 101110 100 1010 101 110100 101111 110110 1100 11010 110100 110100 100 1100 101111 100 101 11010 1010 101 101 1100 11110 11010 110100 11100 101110 101 1010 1101111 100 1010 1111 110101 1011011 110101 1110 1110 1101110 1111 110100 1010 1011010 101110 101111 110101 1010 101 110101 101 10110100 10110101 0 101111 110100 101 10110100 101110 101110


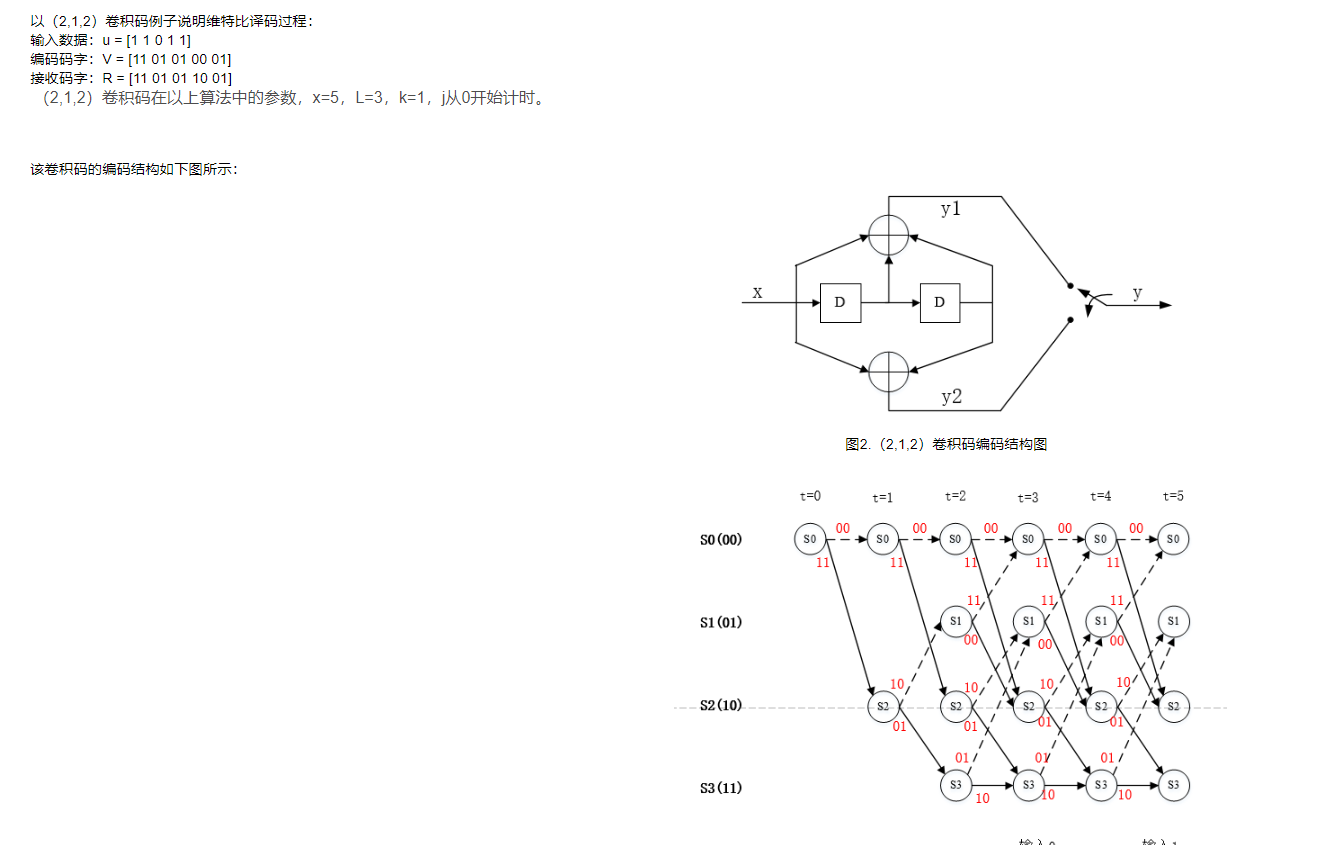
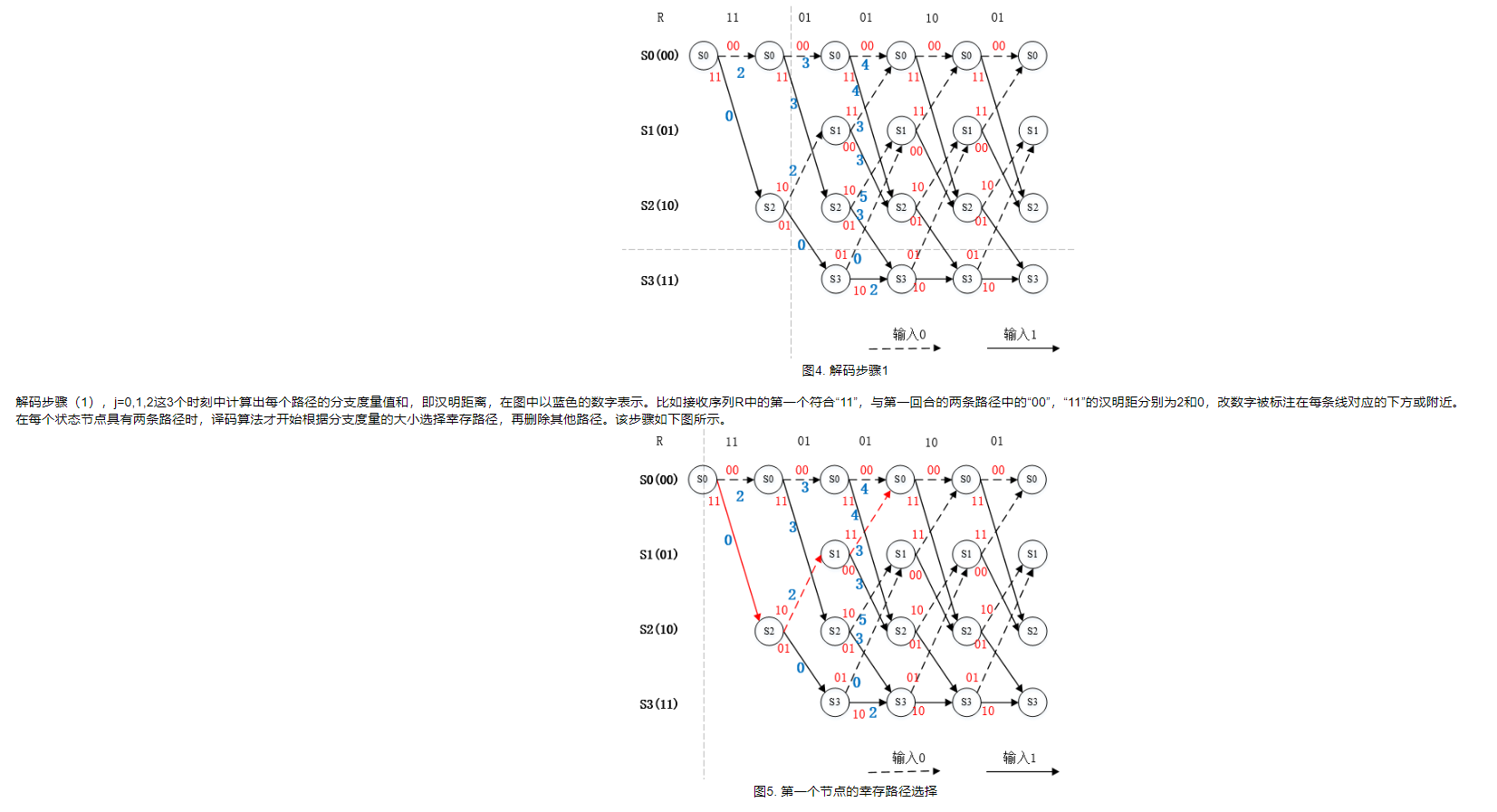
使用Viterbi算法來解碼一個給定的卷積編碼序列。



Viterbi算法是一種動態規劃算法,常用於隱馬爾可夫模型(HMM)中的解碼問題。在這個例子中,假設我們有一個HMM模型,並且我們希望使用Viterbi算法來解碼觀測序列(2,1,2)。
在HMM模型中,我們有以下元素:
現在我們使用Viterbi算法來解碼觀測序列(2,1,2):
max[V[t-1, i] * a(i, j) * b(j, o(t)) for i in States],其中o(t)是第t個觀測值。[V[t-1, i] * a(i, j) * b(j, o(t)) for i in States]。根據上述算法,我們可以進行具體的計算。假設初始概率為π(A)=0.4,π(B)=0.3,π(C)=0.3,狀態轉移概率為A = {{0.2, 0.5, 0.3}, {0.3, 0.1, 0.6}, {0.4, 0.3, 0.3}},觀測概率為B = {{0.5, 0.5}, {0.4, 0.6}, {0.7, 0.3}}。
以下是具體的計算過程:
V[2, A] = max[V[1, A] * a(A, A) * b(A, 1), V[1, B] * a(B, A) * b(A, 1), V[1, C] * a(C, A) * b(A, 1)]
= max[0.2 * 0.2 * 0.4, 0.18 * 0.3 * 0.4, 0.09 * 0.4 * 0.4] = 0.016,BP[2, A] = argmax...
V[2, B] = max[V[1, A] * a(A, B) * b(B, 1), V[1, B] * a(B, B) * b(B, 1), V[1, C] * a(C, B) * b(B, 1)]
= max[0.2 * 0.5 * 0.4, 0.18 * 0.1 * 0.4, 0.09 * 0.3 * 0.4] = 0.04,BP[2, B] = argmax...
V[2, C] = max[V[1, A] * a(A, C) * b(C, 1), V[1, B] * a(B, C) * b(C, 1), V[1, C] * a(C, C) * b(C, 1)]
= max[0.2 * 0.3 * 0.7, 0.18 * 0.6 * 0.7, 0.09 * 0.3 * 0.7] = 0.0378,BP[2, C] = argmax...
V[3, A] = max[V[2, A] * a(A, A) * b(A, 2), V[2, B] * a(B, A) * b(A, 2), V[2, C] * a(C, A)b(A, 2)]
= max[0.016 * 0.2 * 0.5, 0.04 * 0.3 * 0.5, 0.0378 * 0.4 * 0.5] = 0.00256,BP[3, A] = argmax...
V[3, B] = max[V[2, A] * a(A, B) * b(B, 2), V[2, B] * a(B, B) * b(B, 2), V[2, C] * a(C, B) * b(B, 2)]
= max[0.016 * 0.5 * 0.6, 0.04 * 0.1 * 0.6, 0.0378 * 0.3 * 0.6] = 0.004032,BP[3, B] = argmax...
V[3, C] = max[V[2, A] * a(A, C) * b(C, 2), V[2, B] * a(B, C) * b(C, 2), V[2, C] * a(C, C) * b(C, 2)]
= max[0.016 * 0.3 * 0.3, 0.04 * 0.6 * 0.3, 0.0378 * 0.3 * 0.3] = 0.0018144,BP[3, C] = argmax...
因此,觀測序列(2,1,2)的最佳狀態序列為C -> B -> B。
說明Turbo碼的基本結構和工作原理,並給出一個使用Turbo碼進行編碼和解碼的例子。


Turbo碼是一種在數位通信中廣泛使用的錯誤校正編碼技術。它通常應用於具有高容量和高傳輸率的通信系統,以提高可靠性和錯誤率性能。
Turbo碼的基本結構由兩個相同的循環冗余檢查碼(CRC)組成,中間有一個交互解碼器。該結構稱為平行連接結構或串聯結構。
以下是Turbo碼的基本結構和工作原理的解釋:
平行連接結構:Turbo碼的平行連接結構由三個主要組件組成:信息編碼器、交互解碼器和交互結束子。信息編碼器將輸入的信息位串轉換為編碼位串。這個編碼位串由兩個CRC編碼器以平行方式生成。
交互解碼器:兩個CRC編碼器的輸出被交互解碼器使用。交互解碼器通過迭代解碼過程來提高錯誤校正能力。在每次迭代中,它接收解碼結果並生成一個更新的估計結果。這個更新的估計結果通過內部的交互結束子返回給交互解碼器,進一步改進錯誤校正性能。
交互結束子:交互結束子是交互解碼器的一部分,它決定何時結束迭代解碼過程。通常,當迭代次數達到預定值或已經達到可接受的錯誤率時,交互結束子會終止迭代。
工作原理如下:
編碼:輸入的信息位串通過信息編碼器轉換為編碼位串。這個過程包括將信息位串經過兩個CRC編碼器,並將它們的輸出平行連接起來。
解碼:經過編碼的位串在接收端經過通道進行傳輸,並可能受到雜訊和干擾的影響。接收端的交互解碼器開始迭代解碼過程。在每次迭代中,解碼器在每次迭代中,解碼器使用輸入的接收位串和先前的解碼結果來生成一個更新的估計結果。這個估計結果被傳遞給交互結束子。
交互解碼:交互結束子接收更新的估計結果,根據預定的標準(例如迭代次數或錯誤率閾值)來判斷是否結束迭代解碼過程。如果未達到結束條件,則交互結束子將估計結果返回給交互解碼器進行下一次迭代。這個過程將持續進行,直到達到結束條件。
解碼輸出:在迭代解碼過程結束後,交互解碼器將最終的解碼結果生成作為輸出。這個解碼結果可以用來恢復原始的信息位串。
Turbo碼的主要特點是其迭代解碼過程,通過反覆傳遞和改進解碼結果,它能夠提供比傳統的錯誤校正碼更好的性能。Turbo碼已被廣泛應用於數字通信系統,特別是在移動通信標準中,以提供更可靠的數據傳輸和通信品質。
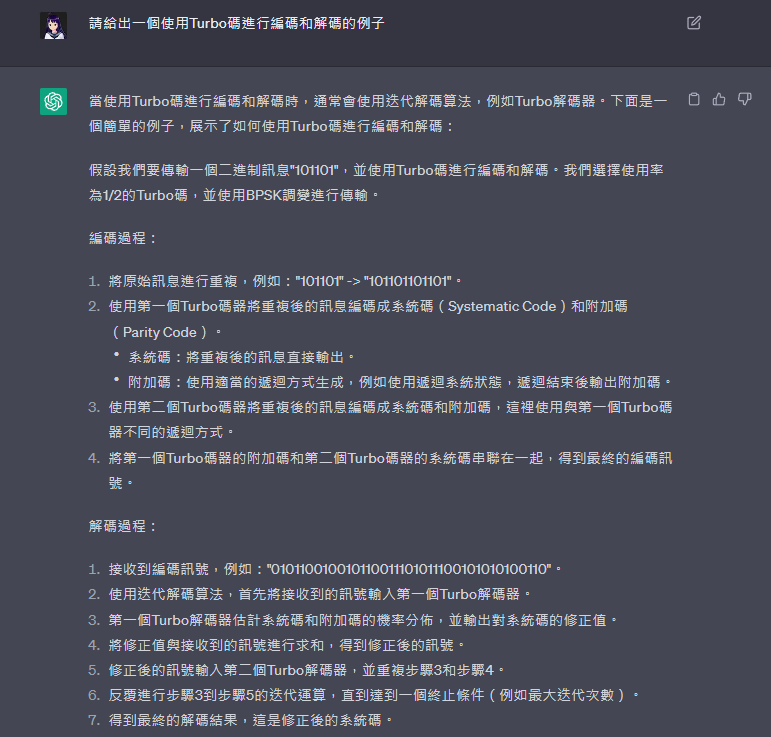
當使用Turbo碼進行編碼和解碼時,通常會使用迭代解碼算法,例如Turbo解碼器。下面是一個簡單的例子,展示了如何使用Turbo碼進行編碼和解碼:
假設我們要傳輸一個二進制訊息"101101",並使用Turbo碼進行編碼和解碼。我們選擇使用率為1/2的Turbo碼,並使用BPSK調變進行傳輸。
編碼過程:
解碼過程:
需要注意的是,上述只是一個簡化的例子,真實的Turbo碼系統中會涉及更多細節和運算。例如,Turbo碼使用的遞迴方式可能是迴旋碼(Convolutional Code)或純位錯誤碼(Block Code),並且會使用適當的調變方式(如BPSK、QPSK等)。
此外,Turbo解碼器還涉及軟判決(Soft Decision)和迭代解碼算法(如BCJR算法),用於估計和修正碼字的機率分佈。迭代解碼的過程中,經過多次迭代,系統碼和附加碼的修正值會逐漸收斂,最終得到較為可靠的解碼結果。
總之,Turbo碼是一種強大的錯誤碼編碼和解碼技術,通常應用於數字通信和無線通信系統中,以提高訊號的可靠性和容錯能力。使用Turbo碼進行編碼和解碼時,需要選擇適當的參數和算法,並進行迭代運算,以獲得更好的解碼效果。




設計一個基於Reed-Solomon碼的錯誤更正編碼方案,並說明其如何檢測和更正錯誤。

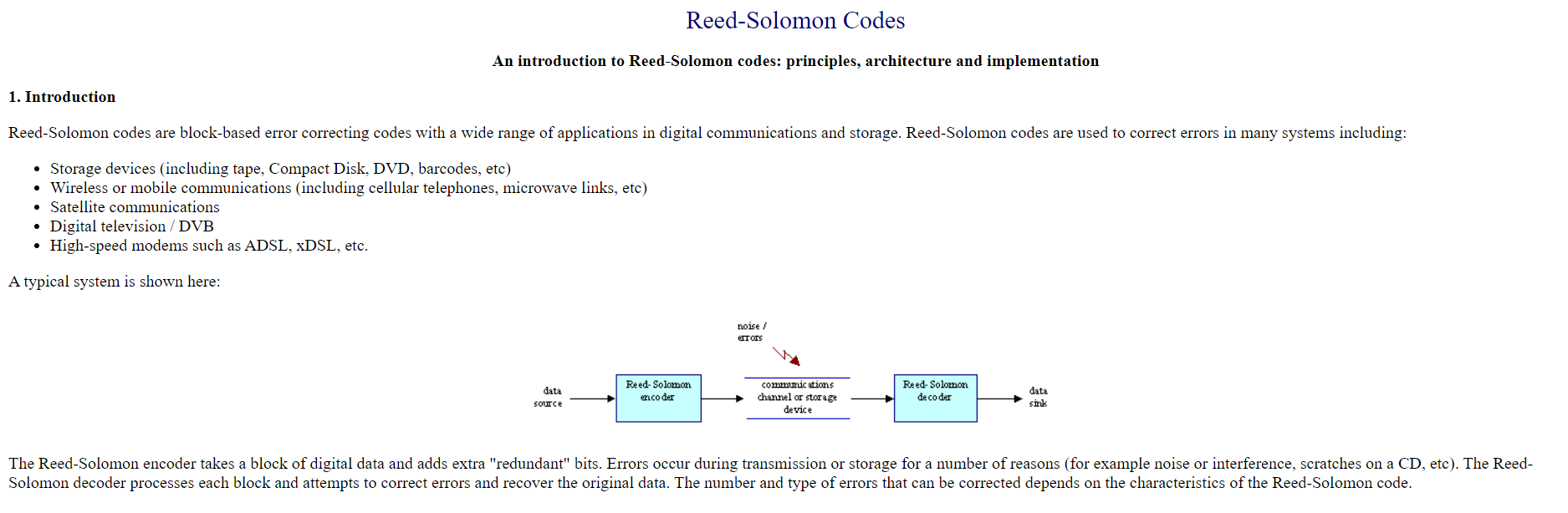
基於Reed-Solomon碼的錯誤更正編碼方案是一種在數據傳輸中檢測和修正錯誤的方法。Reed-Solomon碼被廣泛應用於數據存儲和通信系統中,特別是在光纖通信、衛星通信和數字媒體存儲中。
以下是一個基於Reed-Solomon碼的錯誤更正編碼方案的一般步驟:
確定編碼參數:首先,需要確定Reed-Solomon碼的編碼參數,包括總數據符號的數量(n)、每個數據符號的位元數(k)以及錯誤更正能力(通常表示為t)。
建立生成多項式:根據編碼參數,生成一個稱為生成多項式的多項式。生成多項式的次數為t,並且具有根(稱為根多項式)與所選擇的域上的元素相對應。
數據編碼:將要傳輸的數據劃分為k位元的數據符號。每個數據符號可以表示為多項式形式。將這些數據符號與生成多項式進行多項式乘法,得到一個新的多項式,稱為編碼多項式。
添加紅利符號:根據錯誤更正能力,將編碼多項式的t個係數作為紅利符號添加到數據中。這些紅利符號提供了錯誤檢測和更正的能力。
傳輸數據:將編碼後的數據(包括數據符號和紅利符號)傳送到接收端。
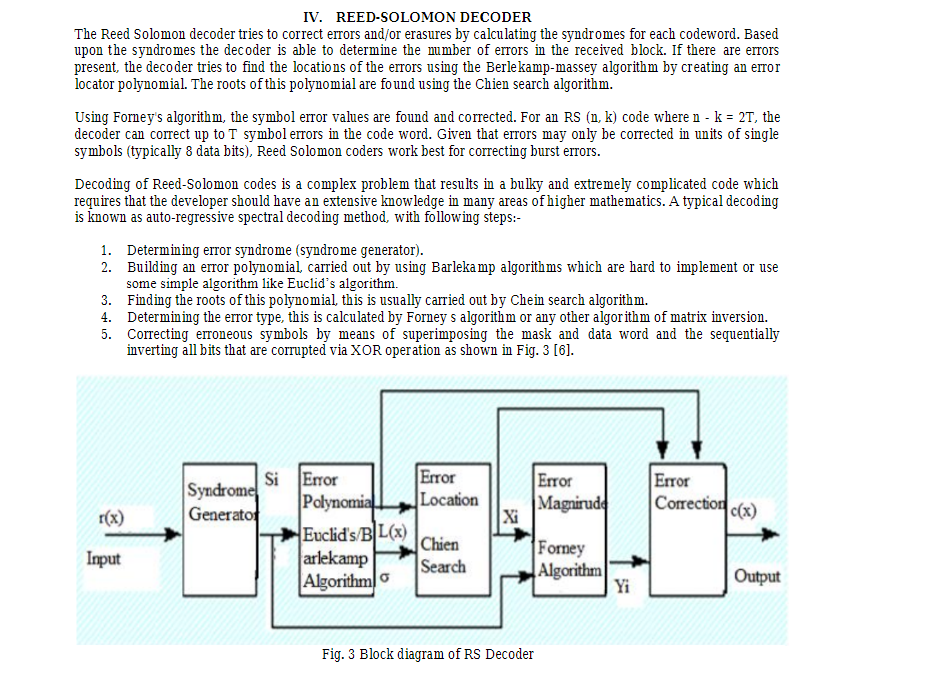
錯誤檢測和更正:在接收端,接收到的數據進行解碼。使用解碼算法(例如Berlekamp-Massey算法或Euclidean算法),檢測和更正錯誤。根據錯誤的性質,可以檢測到的錯誤數量可以達到t或更少。
數據恢復:經過錯誤更正後,可以使用已更正的數據符號進行數據恢復。如果只有少量的錯誤,則可以使用更正後的數據符號重建原始數據。如果無法完全恢復原始數據,則可以使用錯誤檢測和更正機制指示哪些部分存在錯誤,然後採取相應的細化措施,例如重新傳輸或利用冗餘數據進行部分恢復。
Reed-Solomon碼的主要優點是其具有高效的錯誤檢測和更正能力。通過調整編碼參數,可以平衡存儲空間和錯誤更正能力之間的關係。然而,它也有一些限制,例如對於較大的數據塊和高位元錯誤的處理相對複雜。
需要注意的是,上述步驟僅提供了Reed-Solomon碼的一般方案。具體的實現細節可能因應應用場景和具體需求而有所變化。在實際應用中,可能需要考慮其他因素,如交互作用、效能優化和結合其他編碼技術等。建議在實施時參考相關文獻和專業資源,以確保正確且有效的實現。



使用橢圈曲線密碼學Elliptic Curve Cryptography(ECC)對一個訊息(請自行設計)進行編碼和解碼,並說明ECC的安全性特點。



橢圈曲線密碼學(Elliptic Curve Cryptography,ECC)是一種公鑰密碼學算法,用於加密、解密、簽名和驗證等操作。下面是使用ECC對"Hello World"進行編碼和解碼的一個簡單示例:
生成橢圈曲線密碼學的金鑰對(公鑰和私鑰)。
在ECC中,公鑰由曲線上的一個點表示,私鑰是一個隨機數。可以使用不同的曲線和參數來生成金鑰對,這裡我們使用一個簡單的示例橢圈曲線(secp256r1)。
將"Hello World"編碼為一個數字(或稱為明文)。將"Hello World"轉換為數字表示形式,例如使用ASCII編碼,將每個字符映射為對應的數字。
使用私鑰對明文進行簽名。使用私鑰對明文進行數字簽名,簽名過程使用橢圈曲線上的運算。
使用公鑰驗證簽名。使用公鑰對簽名進行驗證,確定簽名的有效性。
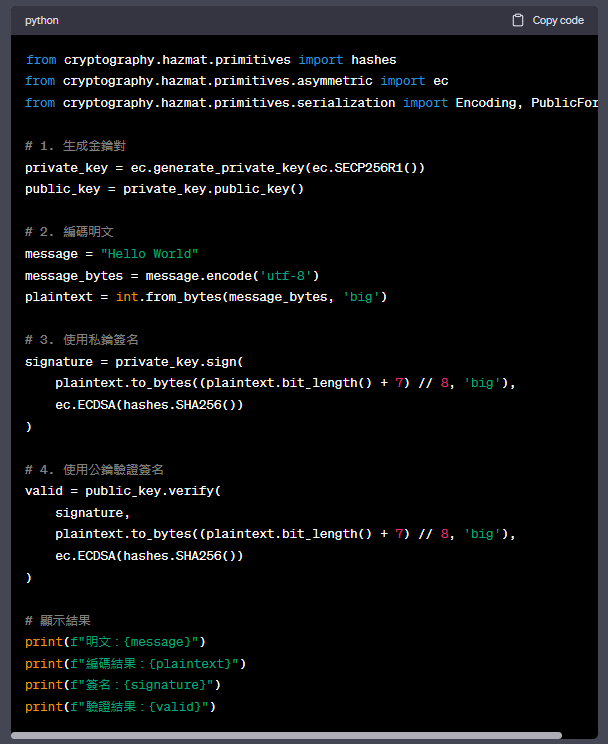
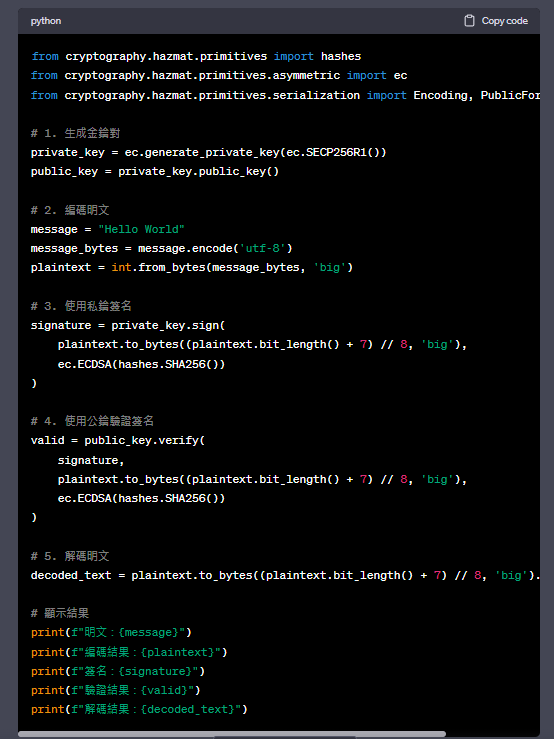
下面是使用Python語言示例代碼,使用橢圈曲線密碼學對"Hello World"進行編碼和解碼:
from cryptography.hazmat.primitives import hashes
from cryptography.hazmat.primitives.asymmetric import ec
from cryptography.hazmat.primitives.serialization import Encoding, PublicFormat
# 1. 生成金鑰對
private_key = ec.generate_private_key(ec.SECP256R1())
public_key = private_key.public_key()
# 2. 編碼明文
message = "Hello World"
message_bytes = message.encode('utf-8')
plaintext = int.from_bytes(message_bytes, 'big')
# 3. 使用私鑰簽名
signature = private_key.sign(
plaintext.to_bytes((plaintext.bit_length() + 7) // 8, 'big'),
ec.ECDSA(hashes.SHA256())
)
# 4. 使用公鑰驗證簽名
valid = public_key.verify(
signature,
plaintext.to_bytes((plaintext.bit_length() + 7) // 8, 'big'),
ec.ECDSA(hashes.SHA256())
)
# 5. 解碼明文
decoded_text = plaintext.to_bytes((plaintext.bit_length() + 7) // 8, 'big').decode('utf-8')
# 顯示結果
print(f"明文:{message}")
print(f"編碼結果:{plaintext}")
print(f"簽名:{signature}")
print(f"驗證結果:{valid}")
print(f"解碼結果:{decoded_text}")
在這個補充的代碼中,我們添加了第5個步驟,即解碼明文。我們將編碼後的明文轉換回原始的字符串形式,並將其存儲在decoded_text變量中。
輸出結果會顯示明文、編碼後的數字、簽名、驗證結果和解碼後的明文。請注意,簽名和驗證是使用私鑰和公鑰進行的,用於確保消息的完整性和身份驗證。
橢圈曲線密碼學(Elliptic Curve Cryptography,ECC)具有以下安全性特點:
安全性強:ECC提供與其他公鑰加密算法相當的安全性,但使用更短的金鑰長度。相比於傳統的RSA算法,使用相同的安全強度,ECC金鑰可以更短,從而提高效率和節省存儲空間。
計算效率高:ECC在相同的安全強度下,需要更少的計算量和存儲空間。因為ECC的運算是基於橢圈曲線上的點的運算,而點運算通常可以在較小的位元組上進行,這使得ECC在資源有限的環境中表現出色,如行動設備和嵌入式系統。
抗量子計算攻擊:ECC對量子計算機的攻擊具有抵抗力。傳統的公鑰加密算法,如RSA,基於大整數分解問題,可以在量子計算機上被迅速破解。而ECC基於橢圈曲線上的離散對數問題,對量子計算機的攻擊更加困難,需要更大的量子位元組才能破解。
鍵尺寸小:ECC相比於其他公鑰算法,使用較小的金鑰尺寸來達到相同的安全強度。這對於嵌入式設備和低帶寬環境非常有利,可以節省計算和通信成本。
簽名效率高:ECC的簽名操作相對高效,需要的計算量和資源較少。這使得ECC在需要高效率的數字簽名應用中特別有用,如安全通信和數位證書。
需要注意的是,ECC的安全性仍然取決於使用的曲線和金鑰長度的選擇,以及實現的正確性。使用強大且適當的曲線參數以及適當的金鑰管理實踐對於確保ECC的安全性至關重要。



Faculty of Informatics Masaryk University-Elliptic curves cryptography and factorization

Faculty of Informatics Masaryk University-Elliptic curves cryptography and factorization
比較馬可夫鏈(Markov Chain)和隱馬可夫模型(Hidden Markov Model)在自然語言處理中的應用,並說明它們在編解碼中的作用。
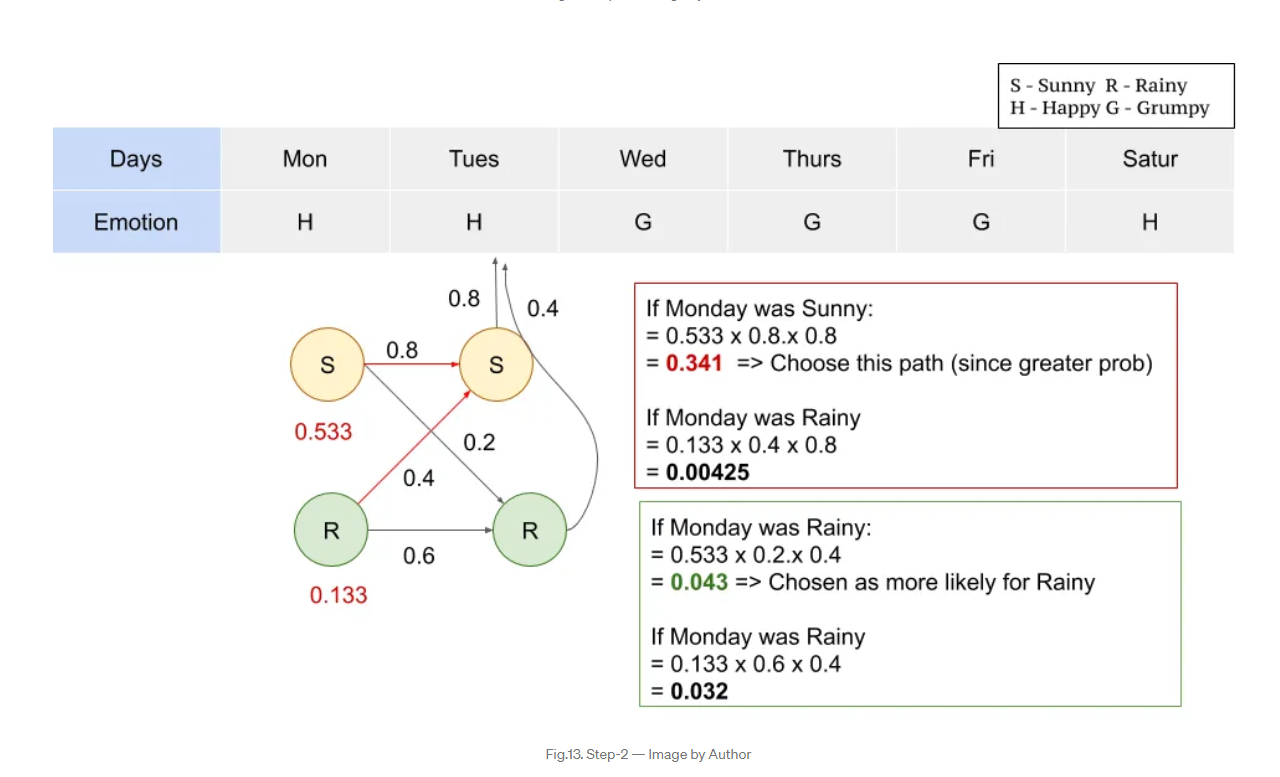
馬可夫鏈(Markov Chain)和隱馬可夫模型(Hidden Markov Model)都是統計模型,它們都可以用來描述一個含有隱含未知參數的馬可夫過程。在正常的馬可夫模型中,狀態對於觀察者來說是直接可見的,這樣狀態的轉換機率便是全部的參數。而在隱藏式馬可夫模型中,狀態並不是直接可見的,但受狀態影響的某些變數則是可見的。每一個狀態在可能輸出的符號上都有一機率分布。因此輸出符號的序列能夠透露出狀態序列的一些資訊。
在自然語言處理中,隱藏式馬可夫模型被廣泛用於語音辨識、中文斷詞/分詞或光學字元辨識等領域1。而馬可夫鏈也有眾多的生物學應用,特別是增殖過程,可以幫助模擬生物增殖過程的建模。
馬可夫鏈(Markov Chain)和隱馬可夫模型(Hidden Markov Model)都可以用於編解碼。隱馬可夫模型是一種統計模型,它用來描述一個含有隱含未知參數的馬可夫過程。其難點是從可觀察的參數中確定該過程的隱含參數。然後利用這些參數來作進一步的分析,例如圖型識別。
HMM有三個典型問題: 預測 (filter)、平滑 (smoothing)、解碼 (most likely explanation)。解碼問題是已知模型參數,尋找最可能的能產生某一特定輸出序列的隱含狀態的序列。通常使用Viterbi演算法解決。

What Is the Difference Between Markov Chains and Hidden Markov Models?


說明如何使用循環冗餘校驗(Cyclic Redundancy Check, CRC)來檢測數據傳輸中的錯誤,並提供一個CRC-32編解碼的例子。



循環冗餘校驗(Cyclic Redundancy Check, CRC)是一種常用的錯誤檢測機制,用於檢測數據在傳輸過程中可能發生的錯誤。CRC使用數學算法來生成一個檢測碼,並將該檢測碼附加到要傳輸的數據中。在接收端,同樣的算法應用於接收到的數據,並與接收到的檢測碼進行比對,以檢測是否存在錯誤。
下面是使用CRC檢測錯誤的一般步驟:
選擇CRC多項式:首先,需要選擇一個CRC多項式。CRC多項式的選擇取決於具體的應用場景和數據傳輸協議。常見的CRC多項式包括CRC-8、CRC-16和CRC-32等。
生成檢測碼:在傳送數據之前,需要計算數據的檢測碼。將數據視為一個二進制數,將CRC多項式作為除數,對數據進行除法運算,得到餘數。這個餘數就是檢測碼,它會被附加到原始數據的末尾。
傳輸數據:將原始數據連同檢測碼一起傳輸到接收端。可以將數據和檢測碼組合成一個數據包或者封包,以便整體傳輸。
檢測錯誤:在接收端,接收到數據後,使用相同的CRC多項式對接收到的數據進行除法運算。如果除法的結果為0,則表示沒有錯誤;如果結果不為0,則表示數據在傳輸過程中發生了錯誤。
處理錯誤:如果檢測到錯誤,則需要採取相應的錯誤處理措施。這可能包括重新傳輸數據、要求數據發送端重發數據等。
值得注意的是,當檢測到錯誤時,可以使用以下方法來處理錯誤:
重新傳輸數據:如果檢測到錯誤,接收端可以通知發送端重新傳輸數據。這可以通過通信協議或其他通信機制來實現。
要求數據發送端重發數據:接收端可以向數據發送端發送錯誤通知,要求其重發相應的數據。這通常在通信協議中有相應的機制來處理。
使用前向錯誤更正(Forward Error Correction, FEC):FEC是另一種錯誤檢測和修正的技術。與CRC不同,FEC可以在接收端直接修復部分錯誤,而不需要重新傳輸數據。它通常基於冗余的數據和錯誤校驗碼,可以檢測和修正一定數量的錯誤。
紀錄錯誤:即使數據在傳輸過程中檢測到錯誤,也可以記錄這些錯誤以進行後續的故障排查和分析。這對於檢測可能存在的問題或通信環境的改進非常有用。
需要注意的是,CRC只能檢測錯誤,而不能修正錯誤。它可以有效地檢測出大多數錯誤,但並非絕對可靠。適當地選擇CRC多項式和適當的錯誤處理機制對於確保數據的可靠傳輸至關重要。
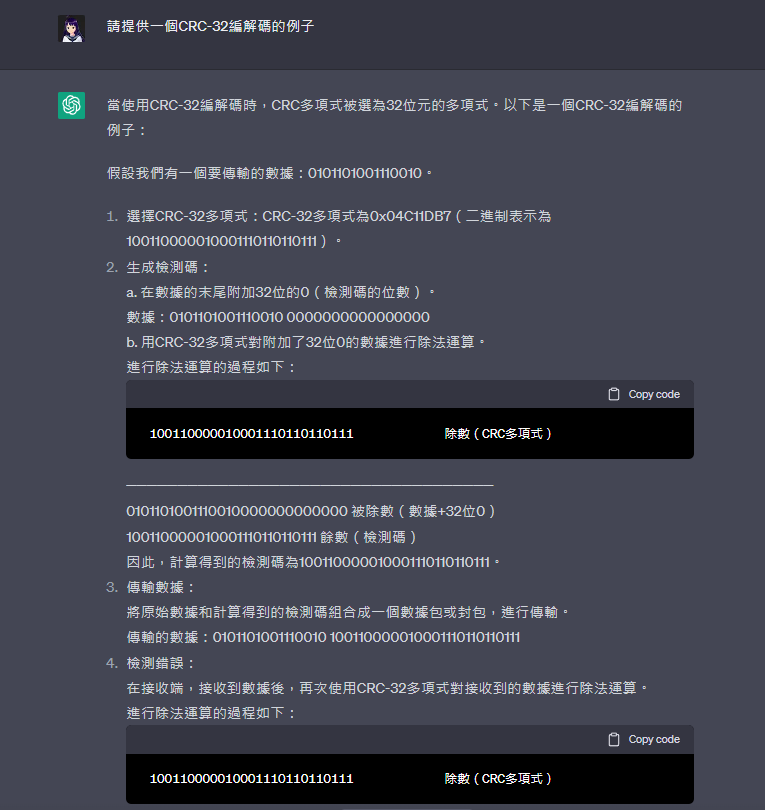
當使用CRC-32編解碼時,CRC多項式被選為32位元的多項式。以下是一個CRC-32編解碼的例子:
假設我們有一個要傳輸的數據:0101101001110010。
選擇CRC-32多項式:CRC-32多項式為0x04C11DB7(二進制表示為100110000010001110110110111)。
生成檢測碼:
a. 在數據的末尾附加32位的0(檢測碼的位數)。
數據:0101101001110010 0000000000000000
b. 用CRC-32多項式對附加了32位0的數據進行除法運算。
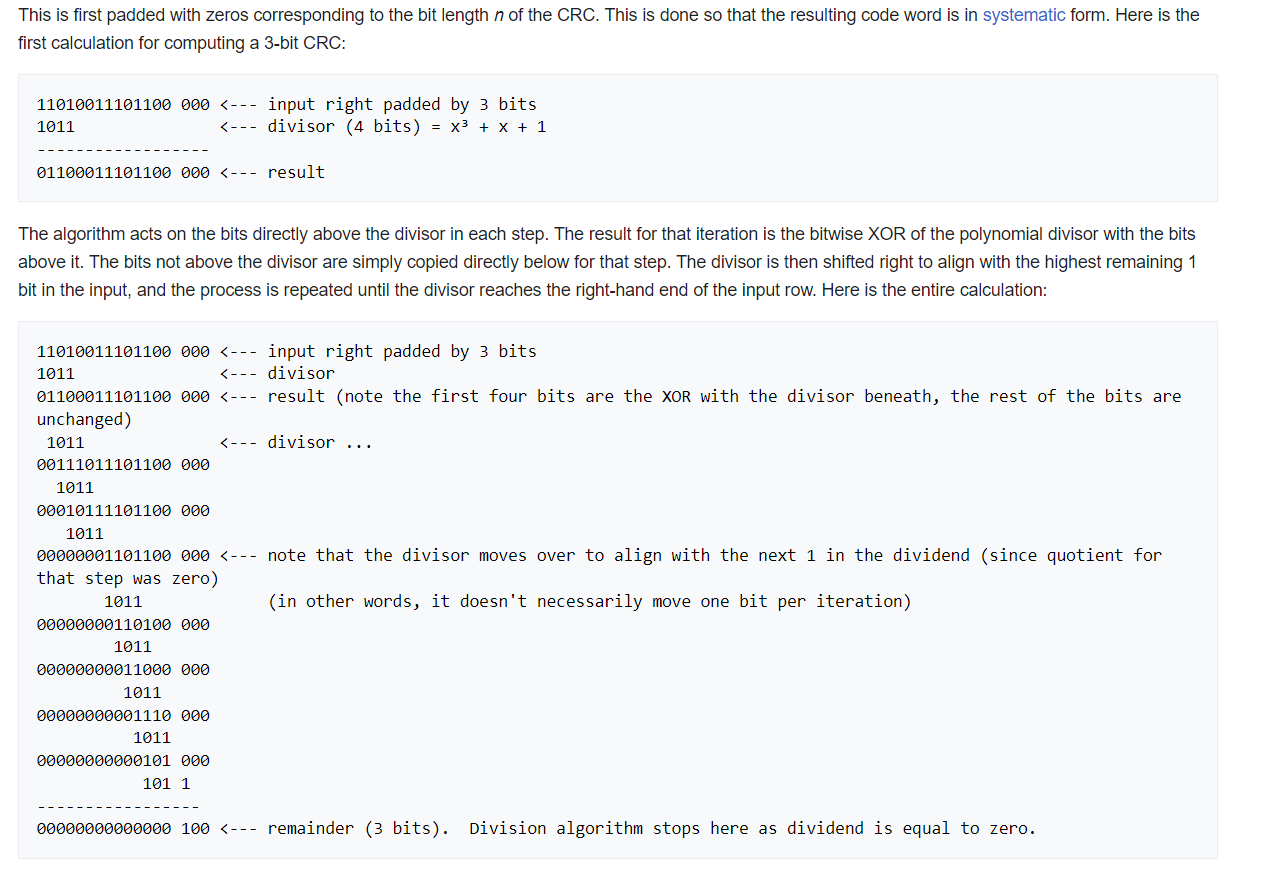
進行除法運算的過程如下:
100110000010001110110110111 除數(CRC多項式)
────────────────────────────────────
0101101001110010000000000000 被除數(數據+32位0)
100110000010001110110110111 餘數(檢測碼)
因此,計算得到的檢測碼為100110000010001110110110111。
傳輸數據:
將原始數據和計算得到的檢測碼組合成一個數據包或封包,進行傳輸。
傳輸的數據:0101101001110010 100110000010001110110110111
檢測錯誤:
在接收端,接收到數據後,再次使用CRC-32多項式對接收到的數據進行除法運算。
進行除法運算的過程如下:
100110000010001110110110111 除數(CRC多項式)
────────────────────────────────────
0101101001110010100110000010001110110110111 被除數(接收到的數據)
100110000010001110110110111 餘數
如果餘數為0,則表示沒有錯誤;如果餘數不為0,則表示數據在傳輸過程中發生了錯誤。
請注意,上述例子僅為CRC-32的一個簡單示例,實際應用中可能涉及到更複雜的數據和計算過程。


這次的作業中,從各個面向的題目與以GPT+Bing作回答的過程中,自己充分體會到生成式AI帶來的便利,跟以往在網Google上搜尋資料不同的是,我們可以針對同個問題進行更深入的連續對答,且藉由GPT作為初步把關也可以省去絕大部分在茫茫links中尋找相關知識的時間,而且它在範例程式碼所提供的資源也十分令人驚艷,不但是跨了多種程式語言、且只要下對基本的Key Word,它便可以回覆具有初步卻又有足夠完整性的架構。
而在有了這樣的得力工具後,相信人們也能省去許多不必要的時間,在廣闊的知識大海上,我們可以不用不斷地被卡在"造輪子"的階段裹足不前,也更能往更深入、需要更多思考的層面邁進,讓歷史上科技沉靜已久的齒輪重啟、跨入下個重大的科技革命!
